FUZZIFIER
L ’ ARCHITECTURE
ETUDE DE LA
LOGIQUE FLOUE ET DES SES APPLICATIONS DANS L ’ ARCHITECTURE
Personne n’a su ériger l’Architecture en Science, alors adaptons les Sciences à l’Architecture
Directeur de Mémoire : Monsieur Alain Constans.
Merci à :
Anne pour sa générosité hors du temps.
Le mémoire de quatrième année est une étape importante au des études d’architecture. Il a pour vocation de permettre à l’élève de produire un « travail personnel identifiable[1]»
Attiré par les sciences en général et l’informatique en particulier, je ne voyais pas l’intérêt de produire un mémoire consacré à « l’informatique appliquée à l’architecture » ni sur « le renouveau de l’architecture par l’ordinateur ». Je souhaitais suivre une voie assez pointue et surtout peu connue des sciences qui me permettrait de mettre en avant mes capacités scientifiques, professionnelles et mes capacités pédagogiques dans le but de faire découvrir quelque chose. Après quelques tentatives infructueuses, une idée de recherche m’a paru satisfaire ces trois buts : L’étude de la logique floue*, logique ayant pour but de rendre la pensée scientifique plus « humaine ». Si, au terme de ce mémoire, je parviens à mélanger les trois genres alors je pense que je serais parvenu à mon but premier :
Être apte a suscité l’intérêt auprès de mes lecteurs
2. Rappel theorique sur les ensembles
5. Quand la logique trouve ses limites
1. Des avantages oui, mais lesquels ?
2. Une application professionnelle
« L’architecture, c’est moche ! »
Qui parle ainsi? Un fou ? Une personne qui hait les sciences et l’art ? Ou un Homme, tout simplement ?
Une telle exclamation exempte de logique ôte tout crédit à son auteur. Une affirmation similaire soutenue par un raisonnement logique aurait au contraire mis son idée en exergue.
C’est grâce à cette logique justement, qui existe depuis 2400 ans (merci Aristote*), que nous avons pu acquérir des connaissances sûres et vérifiables. Ces connaissances logiques sont un enchaînement de raisonnements basés sur des postulats*. Les Postulats de la géométrie Euclidienne par exemple. Puis, un jour, quelqu’un s’est amusé à changer ces postulats et cela a donné naissance à une nouvelle géométrie, ainsi le blanc devient noir et le noir devient blanc. Mais, au final, cela fait 2400 ans que l’on perd de vue le principe même qui a créé cette logique : Comprendre le monde alentour. Et lorsque l’on essaye, le monde apparaît non pas tout blanc ni tout noir mais évidement gris. Le vrai se mélange au faux contrairement au 0 qui s’oppose au 1. Alors pourquoi avoir créé une logique hors du monde ? D’accord il fallait bien commencer, mais au final, n’a-t-on oublié le principal à savoir le « peut être » et le « partiellement » qui apportent une toute nouvelle dimension aux idées.
C’est alors qu’il devient intéressant de remettre en cause la logique absolue et de faire intervenir une logique plus humaine et moins contraignante. Ainsi, la logique dite « floue » trouve naturellement sa voie parmi les sciences appliquées, permettant d’éviter le carcan trop étouffant de la Science pure. En fait, Il faut voir dans la logique floue une démarche intellectuelle logique qui permet de résoudre des problèmes de façon simple et humanisée. Par contre, elle nécessite l’avis d’expert, non en logique mais dans le domaine concerné d’où l’intérêt qui apparaît d’initier et de former les architectes au flou.
Pour cela, il faut d’abord comprendre la logique bivalente* pour ensuite aborder une logique plurivalente*, la logique floue*. Enfin, il s’agit de l’appliquer à l’architecture et d’en tirer les programmes informatiques avec les bases acquises. Ainsi tout ce que peut nous apporter cette nouvelle démarche aura été entrevu.
1. Aristote et les
ensembles
La logique est une démarche de pensée.
« Logique » vient du grec « logos » : la parole, le verbe et ses balbutiements sont à imputer à un philosophe grec : Aristote*. Aristote a consacré sa vie à tenter d’expliquer (et de rationnaliser) la Nature en classant et codifiant tout ce qui la constitue.
« Tous les Hommes sont mortels.
Platon est un Homme.
Donc Platon est mortel. »
Ce syllogisme bien connu, a formalisé un courant de pensée qui est maintenant tellement ancré en nous que l’on ne parle même plus de logique mais d’évidence. Le concept bivalent* du vrai et du faux, du bien et du mal est ainsi apparut et on le retrouve exprimé par les plus grands philosophes comme Descartes pour qui la raison est la « puissance de bien juger, et distinguer le vray d’avec le faux[2] ». Ce n’est qu’à la fin du 19ème siècle qu’un mathématicien du nom de Georg Cantor met en place la théorie des ensembles qui est le support mathématique du concept de vrai et faux.
Figure 1 – Concept de la théorie des ensembles
Malgré son apparente simplicité, ce schéma résume a lui tout seul la logique aristotélicienne. Cependant, afin de mieux le comprendre et pour approfondir un peu cette logique apparemment si naturelle, un petit résumé sur les ensembles est nécessaire.
2. Rappel
theorique sur les ensembles
Le principal postulat* à connaître est le principe du tiers exclus* qui peut s’énoncer ainsi :
Une propriété (p) ne peut que être vraie ou fausse mais jamais
simultanément vraie et fausse.
A partir ce cette simple phrase, on peut construire toute la logique bivalente*
On peut traduire ce tableau par : un ensemble ET son contraire n’ont pas d’élément commun et un ensemble OU son contraire forme le tout ; c’est logique.
|
|
|
|
|
|
|
|
|
V |
V |
F |
V |
V |
V |
V |
|
V |
F |
F |
F |
V |
F |
F |
|
F |
V |
V |
F |
V |
V |
F |
|
F |
F |
V |
F |
F |
V |
V |
V = vrai ; F = faux ; 
= non p ; 
= p et q ; 
= p ou q ;
= si p alors q ; 
= p si et seulement si q
Figure 2 - Tableau de la théorie des Ensembles
Voila le tableau à partir duquel fonctionne tout ordinateur : Ce sont les opérations logiques de négation, d’union, d’intersection et d’implication. Pour le comprendre il faut le lire à haute voix : si P est vrai et Q vrai ? Le contraire de P est faux, P et Q est vrai, P ou Q est vrai etc.….Ce qu’il faut en retenir, c’est que nous n’avons pas le choix, une propriété est vraie ou fausse ; un ordinateur traduit cela par des 1 ou 0.
Souvent confondues avec la logique et encore plus avec la logique floue, les probabilités ont leurs subtilités qui les différencient bien.
3. C’est
Probable
Définition : Une mesure de probabilité P est une application de l’ensemble des événements dans l’intervalle [0,1] qui satisfait aux deux propriétés suivantes :
Ce qui veut dire que si on a deux ensembles distincts (sans élément commun), alors la probabilité de A et B est égal à la somme des probabilités de A et B. De plus :
En somme, la probabilité d’un événement certain est égale à 100%, celle
d’un événement impossible est de 0% et, enfin, si un événement a 30% de risque
de survenue, il a par là-même 70% de chance de ne pas se produire.
4. Envahie
par la logique
Ce bref résumé théorique peut paraître très rébarbatif, mais, il est étonnant de remarquer que toutes ces notions abstraites sont utilisées quotidiennement de façon très concrète. En effet, qui ne s’est jamais posé de question se référant aux calculs de probabilité? Il suffit de jouer aux dés pour appliquer déjà bien plus que ce qui a été exposé précédemment. Que dire alors des courses hippiques ? Les enfants, dès dix ans, aiment, de même, à créer des syllogismes semblables à celui de Platon. L’ordinateur, quant à lui, est une application « sans nulle fantaisie » du tableau de la théorie des ensembles. On peut même dire que la base d’un ordinateur n’est qu’une série de trois opérations basics : ET, OU , NON. Grâce à cela, il calcule additions, soustractions et toutes les combinaisons imaginables. Les systèmes experts en sont l’une des applications les plus prometteuses: Ces programmes permettent de résoudre des problèmes complexes en posant des questions dont les réponses sont simplement oui ou non. Ainsi, un système expert concernant le fonctionnement des véhicules automobiles permettra-t-il de découvrir d’où vient une panne en formulant ainsi ses questions :
_La voiture démarre-t-elle ?
_Si non, le démarreur fonctionne-t-il ?
_Si non, la batterie est-elle branchée correctement ?
_Si oui, alors la batterie est vide.
5. Quand
la logique trouve ses limites
Ainsi, la logique paraît innée et servir à chaque
instant; cependant, à l’observer de plus près, les enfants n’ont pas cette
capacité logique, elle est remplacée par l’intuition. En plus elle ne nous est
utile que dans des cas très simples, ne présentant ni contraintes multiples ni
caractère bien précis. Un raisonnement de départ basé sur la logique simple,
évolue ensuite vers une conception
beaucoup plus personnelle : S’expriment alors toute l’originalité de
l’être humain, son particularisme et éventuellement tout son génie.
Ainsi, en architecture, la notion d’ensoleillement ou la
réalisation d’une esquisse ne répondent
pas à une logique parfaite, de même l’estimation de la qualité globale d’un
bâtiment.
Et l’homme supporte mal la logique « bête et
méchante » d’un ordinateur : Qui n’a jamais perdu patience face à
cette pure logique « mécanique » ?
A une échelle humaine, un système expert par exemple appliqué, comme il en existe, à l’analyse d’une maladie, donne le type de réponses suivantes :
_Etes vous malade ?
_Oui (quelle
question !)
_Toussez vous ?
_Oui beaucoup.
_Toussez vous OUI ou NON ?
_Oui (pff).
_Avez vous une toux sèche ou grasse ?
_Un peu sèche.
_Avez vous une toux SECHE ou GRASSE ?
_Ben un peu seche !
FATAL ERROR IN
ANSWER.DLL
On comprendra ainsi que des réponses logiques, limitées à un
OUI ou un NON ne correspondent pas toujours lorsqu’il s’agit de circonstances
humaines ou lorsque que les données ne sont pas absolues; c’est toute la
richesse de notre langage. En effet, pour rendre fine et précise la
compréhension de ce que nous exprimons, nous ajoutons des adjectifs
qualificatifs (grand, long, fin, mince) ou des adverbes (beaucoup, un peu) qui
permettent d’apporter des nuances beaucoup plus subtiles et plus concrètes
qu’une simple affirmation ou négation : C’est toute l’échelle des gris qui
s’oppose au simple choix du blanc ou du noir.
Ainsi, la logique, créée par et pour
l’Homme pour mieux l’aider, trouve-t-elle ses limites au sein des jugements de
valeur de ce même Homme.
Quel modèle scientifique peut s’adapter à une pensée complexe qui désire une expression simplifiée ?
1. Un
peu d’Histoire
Au delà du simple manichéisme qui est l’évolution la plus radicale de la logique et aussi son aboutissement religieux et temporel, on peut se demander où nous mènerait une logique implacable. Tout d’abord, justement à des idées simples puis parfois simplistes et en poussant un peu loin a des idées très populistes. Même si le cartésianisme est un peu galvaudé, il est à la base de beaucoup de courants de pensée. Adopté donc dans de nombreux domaines, son utilisation reste très emblématique d’une société frileuse qui ne veut appliquer que les mathématiques sans équivoque là où le doute subsiste. Et pourtant il n’en reste pas moins que trop de logique tue la logique. Au bout du compte, si il y a bien un domaine où la logique n’a jamais réussi à prendre le dessus c’est dans tout ce qui touche à la beauté, ce qui explique la nécessité d’utiliser d’autres moyen, comme les échelles, pour la définir. Nul n’aurait la prétention ici de parler d’une vraie beauté absolue. Et bien voilà, j’en appelle à définir tout ce qui nous entoure non pas par une logique bivalente* mais plurivalente*. Car quoi de plus humain qu’une langue et quoi de plus complexe que la traduction de ce même langage en données formelles. Et j’irais même jusqu'à « donner aux qualifications des propositions une nuance épistémologique[3]».
Rappelons un philosophe crétois oublié, Epiménide qui pensait que tous les crétois étaient des menteurs. Joli paradoxe que voilà puisque, si Epiménide est crétois, alors il ment et donc tous les crétois disent la vérité et donc Epiménide qui est crétois n’a pas menti ! Ce type de problème irrationnel a poussé les mathématiciens à reconsidérer sérieusement la logique bivalente*. Dans les faits, tout se déclenche au début du siècle dernier, période à laquelle où plusieurs problèmes insolubles apparaissent. En physique par exemple, l’incertitude d’Heisenberg* amène les physiciens à créer le « ½ » en logique pour caractériser ce qui ne peut être déterminé. De même, Lukasiewicz, logicien polonais, en travaillant sur le futur contingent (ce qui est en devenir), est un peu devenu le créateur de la logique plurivalente* puisqu’il faut bien qu’il existe un état qui n’existe pas ET existe simultanément : le futur.
C’est ainsi que, dans les années Trente, Max Back travaille
sur la logique plurivalente appliquée aux ensembles. Mais finalement, ce n’est
qu’en 1965 que Lofti Zadeh, Professeur à l’université de
Berkeley, jette véritablement les bases de la logique floue dans son livre
« Fuzzy set theory ». En 1975, le professeur Mandani réalise le
premier contrôleur flou expérimental dont, quatre ans plus tard, on trouve la première
application dans un four. Depuis, la grande majorité des travaux sur la logique
floue a été menée au Japon où cette théorie est très prisée. Là-bas, il existe
de nombreux ustensiles et appareils électroménagers utilisant cette méthode et
même le fameux métro de Sendai en est dépendant. On peut expliquer ce revirement
des recherches en Orient par le fait que la pensée occidentale est trop marquée
par le cartésianisme qui rend aberrante « la violation du principe
du tiers exclus* » alors que cette idée est
volontiers admise au Japon.
En clair, la logique floue n’est surtout pas une logique
imprécise mais bien une logique qui s’adapte à l’être humain en laissant une
place entre la certitude du vrai et la certitude du faux.
2. Un
peu de théorie
Afin de mieux comprendre, de pouvoir comparer et ensuite d’appliquer ces notions, il est impératif de passer par la théorie.
Au chapitre précédent, une fonction d’appartenance de l’ensemble E,
ne laissait le choix qu’entre 1 ou 0.
Imaginons maintenant A, sous ensemble de E, et une valeur d’appartenance
, de l’élément x dans A, alors :
A est alors un ensemble comme fonction.
Prenons un exemple simple : soit E, l’ensemble des tailles possibles et A le sous ensemble grand. En logique bivalente, on est soit petit soit grand, (x<170cm : pas grand ; x≥170cm : grand). Stupide non ? Si je mesure 170cm, je suis grand et si je mesure 169cm, je suis petit…Cette discontinuité est totalement absurde.
En réalité si je mesure 170cm, je ne suis ni vraiment grand ni vraiment petit ; par contre, si je mesure 175cm, je commence à être sérieusement grand et, au delà de 180cm, je suis vraiment grand. Voila un exemple typique de ce qu’est la logique floue et de son intérêt.
La suite est très simple, il ne reste plus qu’à établir les règles de calcul en logique floue. Elles sont presque toutes analogues à celle de la logique bivalente.
La commutativité, l’associativité, la distributivité et l’involution sont respectées. Cependant, contrairement aux probabilités,
il y a violation du principe du tiers exclus !
D’autre part, la logique floue décrit l’ambiguïté alors que les probabilités décrivent le doute quant à l’occurrence d’un événement. Les opérateurs, quant à eux, sont bien différents. L’opérateur NON est défini ainsi :
L’opérateur OU :
L’opérateur ET :
Voici maintenant, en comparaison de celui de la logique « standard », un tableau récapitulatif.
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
0.8 |
0.5 |
0.2 |
0.5 |
0.8 |
0.2 |
0.8 |
|
0.3 |
0.9 |
0.7 |
0.3 |
0.9 |
0.3 |
0.7 |
Les valeurs données ici sont les valeurs d’appartenance
à un ensemble ;
= non p ; = p et q ; = p ou q ;
Figure 3 - Tableau de la théorie des Ensembles Flous
Ainsi, nous remarquons que si l’on contraint les valeurs à 0 ou 1, la théorie est la même que pour la logique bivalente ; de même, on peut vérifier que le tiers exclus est faux. Nous avons utilisé, pour ce tableau, la méthode de Zadeh, la plus utilisée. Cependant, il existe d’autres méthodes qui permettent de calculer le ET et le OU. Par exemple, la méthode Probalistique dans laquelle OU se calcul par :
Ou encore la méthode de Lukasiewicz dans laquelle ET se calcule par :
L’un des nombreux avantages de la logique floue est aussi que les concepts de très ou très peu existent.
On peut ainsi définir la fonction de concentration (très) comme :
3. Comment
l’appliquer ?
Figure 4 – Régulateur par logique floue
Maintenant, essayons d’appliquer ces concepts au régulateur de température d’un chauffe eau.
Etape n°1 : Définition des entrées et sorties.
En entrée, nous avons la température de l’eau à l’intérieur du ballon et en sortie, l’ampérage à fournir au chauffe-eau. Nous pourrions très bien définir d’autres entrées comme la température extérieure ou celle de la pièce ou les trois à la fois.
Etape n°2 : Fuzzification ou définition des fonctions d’appartenance des variables.
En clair, il s’agit d’attribuer à chaque variable des degrés d’appartenance à différents états que l’on doit définir. Pour simplifier, nous allons définir trois états d’entrée (trop chaud, tiède et trop froid) et trois états de sorties (nul, faible et fort). Maintenant, nous allons établir les degrés d’appartenance à ces états à l’aide de graphique.
Figure 5 - Graphique de fuzzification des variables
Etape n°3 : Création des règles d’inférences*.
Il s’agit tout simplement, comme nous le ferions naturellement, de donner les règles qui lient les données aux actions. Ainsi, si la température est « trop froide », il faut mettre le courant « fort » ; si la température est « trop chaude », il faut mettre le courant sur « nul », et, enfin, si la température est « tiède », il faut mettre le courant sur « faible ». C’est ici qu’intervient tout l’intérêt de la logique floue car ces règles sont établies par le bon sens d’une personne avertie ou experte dans le domaine et non pas par un programmeur. Dans le cas cité, on pourrait prendre l’avis d’un ingénieur en climatisation qui dirait qu’il ne faut pas trop chauffer (notons bien le « pas trop ») lorsque la température extérieure est un peu au dessus de 20°C (« un peu ») et il s’agirait alors simplement de rajouter une règle et d’utiliser une des méthodes de calcul du « ET ».
Etape n°4 : Calcul et défuzzification.
Prenons un exemple simple: l’eau est à 37,5°C.
Figure 6 - Schéma de défuzzification
Une fois les calculs faits, on obtient un schéma de résultat qui n’est autre qu’une valeur floue : la surface hachurée. Il s’agit maintenant de transformer cette valeur floue en grandeur physique réelle. Pour cela il existe trois grandes méthodes :
La méthode du maximum qui correspond à l’abscisse minimum de l’ordonnée maximum de la surface (on trouve 0,75A). Cette technique simple voir simpliste ignore les règles secondaires qui peuvent néanmoins être importantes pour la stabilité du système. Cette technique est peu utilisée.
La méthode de la moyenne pondérée. Il faut simplement cette fois faire la moyenne des résultats en leur attribuant comme coefficient leur validité.
Cette méthode est nettement plus juste et prend en compte tous
les résultats présents malgré quelques ambiguïtés.
La méthode des centroïdes est de loin la meilleure. Elle
consiste tout simplement à calculer le centre de gravité des surfaces. Pour
cela nous calculons les centres de gravité de chaque surface puis nous pondéront
les résultats avec les surfaces.
Figure 7 - Schéma de la méthode des centroïdes
Cette méthode est la plus gourmande en calcul mais donne les résultats les plus justes.
Il n’y a bien sur pas de méthode miracle et on peut encore trouver d’autres méthodes qui nuanceraient le résultat. L’essentiel est d’arriver à trouver une valeur cohérente par rapport a l’utilité que l’on cherche.
1. Des
avantages oui, mais lesquels ?
Abordons les avantages de la logique floue en elle- même.
Déjà, comme nous avons pu le constater, nous n’avons pas eu
besoin d’établir de modèle mathématique de l’ensemble du chauffage. Cela évite
des années de travail sur des modèles, qui au bout du compte n’existent pas
forcement ou sont d’une complexité à faire pâlir les chercheurs dans le
nucléaire.
Ensuite la logique floue permet de prendre en compte les
typologies linguistiques et donc toutes les nuances que l’on a créées dans le
but d’imiter au mieux le réel.
Nous avons pu traiter des systèmes à comportement complexe
(même si l’exemple est simplifié, cela reste un système complexe en mathématique
pure) en restant accessible à tout un chacun.
Nous pouvons aujourd’hui nous servir de solutions matérielles
comme des microprocesseurs uniquement dédiés aux calculs flous, ce qui permet
d’accroître le rendement puisque cela réduit la programmation.
Nous aurions pu augmenter facilement le nombre d’entrées
sans réellement compliquer les calculs (alors qu’en logique simple la taille
des calculs est exponentielle).
Ensuite on peut aussi voir tout les avantages annexes liés à la simplicité de la formulation qui ne nécessite aucun programmeur ultra performant ni algorithmicien de génie mais tout simplement un expert dans le domaine concerné qui a pour simple tache d’énoncer des lois en langage courant avec toutes les nuances qu’il désire. C’est en faite cette phase de la conception qui est primordiale et elle nécessitera une phase de test afin de vérifier la véracité des dires. De même l’ajout ou le retrait de règles ne change quasiment rien au principe alors qu’en logique bivalente, cela peut changer du tout au tout.
Dans la majeure partie des cas, les applications des
concepts flous, portent sur le traitement flou d’informations non floues par
nature, mais entachées d’imperfections apportées par le processus de mesure
(imprécision et/ou incertitude). Cependant, on
rencontre parfois des situations où l’information est floue par
essence : objets (défauts dans le bois), caractéristiques d’objets
(confort d’un siège) ou résultats d’évaluation sensorielle.
2. Une
application professionnelle
« les outils d’analyse sont de plus en plus sophistiqués, basés sur des traitements statistiques, mathématiques, que ce soit de la logique floue ou des approches non déterministes. » Robert Copé dans Techniques & Archi.
« Chercheurs et praticiens ont posé la question de la place de l’instrumentation dans le processus de projet urbain. L’ingénierie de la cohérence mais aussi des modes de raisonnement analogiques comme la logique floue[…] ont été mis en avant » Frédéric Mialet dans AMC.
« un domaine d'application privilégié reste la vision artificielle[…] Nous cherchons à prendre en compte la variabilité de l’environnement et des images pour améliorer les performances des traitements en y introduisant des connaissances contextuelles du problème. L’utilisation des concepts flous permet d’aborder différemment des problèmes tels que la segmentation d’images ou la reconnaissance de formes. Nos travaux se décomposent selon deux actions principales, l'une plus appliquée portant sur les modèles flous, symboliques, l'autre plus méthodologique, concernant l’application des concepts flous à la segmentation d’images et à la reconnaissance de formes.» Brémont, E. Levrat, L. Rondeau, R. Ruelas, A. Voisin Projet de Recherche 1996/2000.
Comme on peut le constater, les domaines d’application de la
logique floue sont vastes et variés, et les recherches dans ce domaine sont
nombreuses. Dès qu’il s’agit d’interagir avec les hommes on peut faire appel à
ces méthodes. Et justement, les endroits dans lesquels nous évoluons sont les premiers
liens que l’homme tisse avec son environnement. Donc la relation avec
L’architecture est évidente. Il s’agit bel et bien d’utiliser des données
floues comme les Hommes, leur confort et l’environnement pour arriver à faire
des Bâtiments dont la logique permet d’améliorer toutes les données de départ.
C’est le principe même du flou.
3. L’architecture
fuzzifié
On peut envisager toutes sortes d’applications liées a l’architecture qui utiliseraient les bases de la logique floue.
Dans l’urbanisme ou la logique floue permettrai envisager autrement les limites des villes et des de quartiers. Des logiciels de calcul de COS prendraient alors en compte réellement l’environnement suivant les choix des urbaniste.
De même on peut imaginer des applications qui établiraient le degré d’appartenance à des normes comme le HQE. Car quoi de plus flou que l’actuelle norme HQE. 14 points qu’il faut essayer d’atteindre. Avec un programme en logique floue il serait très simple de donner les entrées comme les perditions thermique du bâtiment ou d’autres entrée plus subtil comme l’orientation ou l’utilisation de tel matériaux et au final avec quelques règles on pourrais obtenir ou non le label HQE. Cela serait très simple a mettre en œuvre une fois le moteur flou crée.
On pourrait aussi faire des études d’impact des bâtiment ou de façades ou étudier au mieux la gestion des surfaces ou encore évaluer le coût global d’un bâtiment. Enfin bref les applications ne manquent pas.
Une des idées les plus abouties concerne la mise en dessin de croquis d’architectes. Cette idée, sans doute aussi vieille que l’apparition des NTIC* a toujours excité les pensée des architectes. Avec la logique floue on atteint une étape supplémentaire dans cette recherche. Maintenant les démarches humaines utilisées lors de croquis peuvent être interprété par la machine à travers le moteur flou. Le meilleur exemple est le programme Esquise issu de la recherche du groupe Lucid dirigé par Pierre Leclerc.
Ce
logiciel n’a besoin que d’un simple croquis.
Pour arriver a calculer en temps réel :
La
topologie de l’agencement des pièces avec des indications annexes concernant
les formes
De
même qu’une estimation des besoins énergétiques du bâtiment.
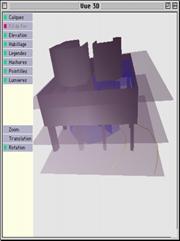Et bien sûr une visualistation 3D en temps reel.
Ainsi le croquis entraîne le dessin et les résultats des calculs influent sur le croquis.
« L’architecture c’est moche »
Cette exclamation existera toujours mais on peut espérer que dire d’un bâtiment qu’il est mal agencé n’existera plus. On pourrait s’approcher de cette utopie en utilisant les ordinateurs a bon escient. Il ne s’agit pas de faire faire un bâtiment à l’ordinateur mais bien de se servir de sa puissance de calcul afin de régler les problèmes techniques (normes, agencement, structure). Ces problèmes n’étaient jusqu'à présent pas abordé parce que cela nécessitait des années de recherches et des quantités de programmes pour arriver à des maigres résultats. Aujourd’hui de nouvelles voies s’ouvrent. Celle de la logique floue par exemple permet d’appréhender des problèmes mathématiques complexe de façon simple et intuitive. La ou des quantités faramineuses de lignes de code et des processeurs ultra puissants sont utiles ; un moteur de logique floue avec son processeur dédié pourrait répondre beaucoup plus vite et simplement en se basant en plus sur l’expérience d’un architectes, plus que sur le talent du programmeur. Ainsi serait redonné aux acteurs principaux le rôle qu'ils ont à jouer dans la création grâce à la maîtrise de leurs outils. On peut espérer qu’avec un architecte maître de tous les aspects, la cohésion globale d’un bâtiment soit assurée et par là-même sa beauté. Avec de tel outils c’est chose assurée.
C'est finalement que juste retour de l’histoire, puisque jusqu'à présent les hommes devaient s'adapter aux outils informatiques, maintenant ce sont les outils qui s'adaptent à l'homme.
1. Livres
Le monde de Sophie
Jostein Gaardner
La logique, informatique et paradoxe
J.P. Delahaye Ed. Pour la sciences Diffusion Belin
La logique ou l’art de raisonner
Y. Delmas-Rigoutsos R. Lalement Ed. Le pommier
La logique Floue : pour les
affaires et l’industrie
Earl D. Cox Thomson publishing
Les systèmes intelligents basés sur la connaissance
W.J. Black Ed. Manson
Une Histoire des Mathématiques, routes et
dédales
Dahan-Dalmedico/J. Peiffer Ed. Points Sciences
Cours Algèbre
Jean Marie Monier Ed. Dunod
Comprendre la logique moderne
F. Chenique Ed. Dunod.
Elément de la logique floue
L. Gascogne Ed. Hermes
Idées nettes sur la logique floue
J. Godjevac Presse Polytechniques et universitaires romandes
Introduction à la théorie des sous
ensembles flous
A. Kaufmann Ed. Masson
2. Magazines
Note de M.Beyhum, 7 octobre 2002
Techniques et Archi oct-nov 2002
« Alchimie du Beton », Robert Copé
AMC n°120 novembre 2001 p38
3. Sites Web
Projet de Recherche 1996/2000
Brémont, E. Levrat, L. Rondeau, R. Ruelas, A. Voisin
http://uranus.cran.uhp-nancy.fr/
Pour y voir plus clair, dans la logique floue !
Bernard Mantel
Introduction à la logique floue
Pierre Gabriel
http://elap.montefiore.ulg.ac.be/fuzzy/
Logique Floue
Eric Brasseur - 1994
http://www.4p8.com/eric.brasseur/lofo.html
Logique Floue
Renald Lehoux - 2000
http://perso.wanadoo.fr/lehoux/
Esquise Sketch Recognition
Pierre Leclercq
http://www.lema.ulg.ac.be/tools/esquise/
Figure 8 - Esquise : le futur ?
Figure 1 – Concept de la
théorie des ensembles
Figure 2 - Tableau de
la théorie des Ensembles
Figure 3 - Tableau de la
théorie des Ensembles Flous
Figure 4 – Régulateur par
logique floue
Figure 5 - Graphique de
fuzzification des variables
Figure 6 - Schéma de
défuzzification
Figure 7 - Schéma de la
méthode des centroïdes
Figure 8 - Esquise : le
futur ?..
Aristote (384 – 322 AV JC) : Elève de Platon il devient après la mort de ce dernier le précepteur d’Alexandre le grand. Il créa une école à Athènes en 334 AV JC. Il cherche à produire un discours capable d’expliquer la nature. Il met en place les règles de ce discours qui sont : la logique « Savoir c’est connaître par le moyen de la démonstration ».
Esquise : Esquise est un
logiciel prototype expérimental de capture et d’interprétation de croquis
d’architecte. Il a été crée par l’équipe de Pierre Leclerc au sein du groupe
Lucid. (www.lema.ulg.ac.be/tools/esquise/
)
Incertitude d’Heisenberg : Cela explique le caractère indéterministe des phénomènes quantiques. Mieux la position d’un corpuscule est définie, plus grande est l’incertitude sur son état de mouvement et inversement.
Logique Floue (n.) : Tout système de calcul où les valeurs ne sont pas précisément déterminées ou dont le système ou les données ne sont pas totalement fiables.
Logique Bivalente : Logique dans laquelle seul les valeurs 1 et 0 ou vrai et faux sont utilisées.
Logique Plurivalente : Evolution de la logique bivalente, dans laquelle on ne se limite plus à deux valeurs mais une infinité.
Non contradiction (principe) : Enoncé en premier par Aristote dans l’Organon sous cette forme, « nous ne pouvons pas dire de quelque chose qu'il est et qu'il n'est pas, dans un même égard et en même temps ».
NTIC : Les Nouvelles Technologies de l’Information et de la Communication. Apparues dans les années 1990, elles désignent l’ensemble des machines électroniques des réseaux et des programmes susceptibles de s’interfacer pour reconnaître, acheminer et traiter des données numériques.
Postulat : Tout principe d'un système déductif qui n'est ni une définition ni une proposition assez évidente pour qu'il soit impossible de la mettre en doute.
Probabilité : voir page 11.
Règles d’inférences : En plus des axiomes d'un système formel, nous avons besoin de règles d'inférence pour tirer des conclusions. Un exemple d'application d'une règle d'inférence est lorsque vous concluez qu'un voisin est à la maison parce que son auto est dans l'entrée.'
Système Expert : Application capable d'effectuer dans un domaine des raisonnements logiques comparables à ceux que feraient des experts humains de ce domaine. Il s'appuie sur des bases de données de faits et de connaissances, ainsi que sur un moteur d'inférence, lui permettant de réaliser des déductions logiques (chaînage avant et arrière). C'est avant tout un système d'aide à la décision.
Tiers exclus (principe) : Toute proposition ne peut être que vraie ou fausse. Ce principe a pour conséquence le principe de non contradiction.